homothétie

homothétie

homothétie [ ɔmɔtesi ] n. f.
• v. 1850; de homo- et gr. thesis « position »
♦ Math. Homothétie de centre O et de rapport k : application qui, à un point M, associe le point M' tel que ' = k.

● homothétie nom féminin (du grec thesis, position) Transformation ponctuelle h d'un espace ponctuel affine E, attaché à un espace vectoriel réel ou complexe, définie à l'aide d'un point A de E, appelé centre d'homothétie, par : h (M) = M′ si et seulement si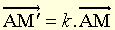 , où k est un scalaire constant, appelé « rapport d'homothétie ». (Notation 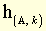.) ● homothétie (expressions) nom féminin (du grec thesis, position) Homothétie vectorielle de rapport α, endomorphisme 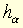défini sur un K-espace vectoriel E (α scalaire non nul) par .

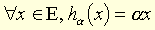homothétie
n. f. GEOM Propriété de deux figures telles que leurs points se correspondent deux à deux sur des droites menées par un point fixe, appelé centre d'homothétie, et que le rapport des distances de ce point à deux points correspondants quelconques soit constant.

⇒HOMOTHÉTIE, subst. fém.
MATH. (géom. projective). Propriété de deux figures dont chaque point de l'une correspond à un point de l'autre sur des droites menées à partir d'un point fixe appelé centre d'homothétie, la distance entre ces points correspondants étant constante. Homothétie directe, inverse. Ayant choisi un point S qu'on nomme centre d'homothétie et un nombre k qu'on nomme rapport d'homothétie ou rapport de similitude, on appelle homothétique d'un point quelconque M le point M' obtenu en joignant SM et prenant à partir du point S, sur cette droite ou sur son prolongement un segment SM' tel que SM'/SM = k (HADAMARD, Géom. plane, 1898, p. 134). L'emploi de la proportion géométrique, qui introduit au point de vue numérique la persistance ou la récurrence d'un rapport donné, introduit au point de vue géométrique et morphologique la similitude ou l'homothétie récurrente des formes (triangles et rectangles semblables) (Arts et litt., 1935, p. 28-06).
Prononc. et Orth. : [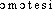] ds Pt ROB. et Lar. Lang. fr.; [-teti] ds LITTRÉ et encore ds WARN. 1968. Selon LITTRÉ, ce serait la prononc. de M. Chasles qui a créé le mot. Elle paraît préférable à DUPRÉ 1972 parce qu'elle correspond au dér. homothétique. Étymol. et Hist. 1872 (LITTRÉ Add.). Dér. régressif de homothétique.

homothétie [ɔmɔtesi; omotesi] n. f.
ÉTYM. V. 1850, mot créé par Chasles (→ Homothétique), in Littré, 1872; de homo-, et grec thesis « position ».
❖
♦ Géom. Transformation géométrique qui, étant donné un point fixe O (centre, pôle d'homothétie) et un nombre k (rapport d'homothétie), fait correspondre à tout point M de l'espace un point M′ tel que : OM′ = kOM. ⇒ Homologue. || L'homothétie est un cas de similitude.
❖
DÉR. Homothétique.

Encyclopédie Universelle. 2012.

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Homothétie — de centre O Dans un espace vectoriel, l’homothétie de rapport k non nul est l application qui à tout vecteur v associe le vecteur kv, où le scalaire k est appelé rapport de l homothétie. Dans un espace affine l’homothétie de centre 0 et de… …   Wikipédia en Français

  • Homothetie — Homothétie Une homothétie est une transformation géométrique d un espace affine dans lui même, fixant un point O appelé centre de l homothétie. Une homothétie se définit par son centre (un point de l espace affine) et son rapport (un scalaire non …   Wikipédia en Français

  • homothétie — (entrée créée par le supplément) (o mo té tie, prononcé ainsi par M. Chasles qui a fait le mot) s. f. Terme de géométrie. Similitude de forme et de position entre deux figures par rapport à un point donné ; l homothétie est directe si les deux… …   Dictionnaire de la Langue Française d'Émile Littré

  • Homothetie — In der Geometrie versteht man unter einer Homothetie eine Affinität, also eine bijektive affine Abbildung eines affinen Raumes A in sich, derart, dass für jede Gerade die Bildgerade f(g) parallel zu g verläuft: Zu den Homothetien zählen genau die …   Deutsch Wikipedia

  • Homothetie (mathematiques elementaires) — Homothétie (mathématiques élémentaires) Fig. 1. L image par une chambre noire correspond à une homothétie de centre la lentille et de rapport négatif. Dans la « vie courante », l homothétie correspond aux agrandissements et aux… …   Wikipédia en Français

  • Homothétie (mathématiques élémentaires) — Dans la « vie courante », l homothétie correspond aux agrandissements et aux réductions. Article détaillé : homothétie. Définition Soit un point M,un point O et un nombre k. On dit que le point M est l image du point M par l… …   Wikipédia en Français

  • Rapport Homothétique — Homothétie Une homothétie est une transformation géométrique d un espace affine dans lui même, fixant un point O appelé centre de l homothétie. Une homothétie se définit par son centre (un point de l espace affine) et son rapport (un scalaire non …   Wikipédia en Français

  • Rapport homothétique — Homothétie Une homothétie est une transformation géométrique d un espace affine dans lui même, fixant un point O appelé centre de l homothétie. Une homothétie se définit par son centre (un point de l espace affine) et son rapport (un scalaire non …   Wikipédia en Français

  • hétie — homothétie prophétie …   Dictionnaire des rimes

  • Plan affine arguésien — Axiome de Desargues Dans une approche axiomatique de la géométrie, un plan affine arguésien (ou desarguésien, ou de Desargues) est un plan affine vérifiant, en plus des axiomes d incidence, l axiome de Desargues : Pour toutes droites d1 …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”